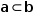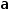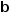2.10.3 Binary operators
Unless otherwise noted, the operators in Figure 2.54 all have binary infix notation. Where the result type is indicated as "o", the type is determined by the type of the operands.
| Name | Symbol | Result | Operands |
| Angle | ∠ | . | ɽ ƈ ʋ |
| Binomial Coefficient | ɓ | . | . |
| Boolean | ∨, ∧, ⊕, ⇒ | . | . |
| Cross Product | × | o | ɽ ƈ ʋ ɱ |
| Concatenate | ‖ | ʈ ɱ ɗ | . ⅈ ɽ ƈ ʋ ʂ ʈ ɱ ɗ |
| Concatenate | ‖‖ | ɱ | . ⅈ ɽ ƈ ʋ ʂ ʈ ɱ ɗ |
| Containment | ∈, ∉ | ɱ | ʂ ʈ ɱ |
| Equivalence | =, ≠, ≈, ≡ | b | . ɽ ƈ ʋ ʂ ʈ ɱ ɗ |
| Inverse | ^-1 | ɱ | ɱ |
| Log | log(b,s) | . | . |
| Lookup | @ | o | ʈ ɱ |
| Matrix Product | × | ɱ | ɱ |
| Numeric | +, -, ⋅, ÷, /, //, ¦, ^, √ | o | . ⅈ ɽ ƈ ʋ ʂ ʈ ɱ |
| Outer Product | ⊗ | ɱ | ɽ ƈ ʋ ɱ |
| Partition | ↓ ↑ | o | ʈ ɱ ɗ |
| Plus or Minus | ±, ∓ | . | . |
| Relational | <, ≤, >;, ≥ | b | . ɗ |
| Scalar Product | × | . | ɽ ƈ ʋ |
| Set | ∪, ∩, ∖, ⊂, ⊆, ⊄, ⊈ | o | ʂ ʈ |
| Vector Product | ∘ | o | ƈ ʋ ɱ |
The usual arithmetic operations such as add and multiply can be applied in mixed mode with one real operand and the other a component or collection operand. The real operand distributes by supplying a copy of the real for each item in the collection and applying the binary operation between the two. Between collections of the same type with the same common type, the binary operators apply to corresponding items of the two collections. Between collections of different types, one of the collections is boxed and treated like a real. The boxed collection is the one whose type matches the common type of the other collection. Between vectors of different types, the operand with lower type is coerced to the type of the other operand. For real mixed with radial, the radial is coerced to vector, the operation applied, and the result coerced back to radial.
Angle
produces the angle between two radials or vectors.
For 2-D radial
operands, this is simply the difference between the angles.
For mixed
operands, the operand with lower type is coerced to vector and the
result
is the arcsin of the dot product of the two vectors divided by
the product of their magnitudes.
That is,
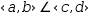



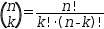
Boolean operators perform Boolean conjunction (∧), addition (⊕), disjunction (∨), and implication (⇒) on Boolean operands, treating 0 as false and any other real value as true. The operators have different precedence, the first three being categorized along with exponentiation, multiplication and addition respectively. The latter has the lowest precedence of all the binary operators.
Concatenate produces a string, matrix or tuple depending on the highest type. String concatenation coerces a non-string operand to string using the operand's parsable representation. Matrix concatenation coerces a tuple to a one-row matrix and any other type to a singleton matrix. Tuple concatenation coerces a non-tuple operand to a singleton tuple. For concatenation of matrices, the shorter matrix is extended with rows containing zeroes.
Concatenate Vertical ‖‖ always produces a matrix. The narrower matrix is extended with rows containing zeroes.
Containment tests its right-operand collection for membership of its left operand. The left operand can have any type.
The Cross operator performs different operations depending on its operands. This operator is inferred when the multiplication operator appears with operands as defined here.
If the operands are vectors the operator constructs the vector product and is defined only for 3-component vector operands. The vector product is defined as a vector that is perpendicular (orthogonal) to the two operand vectors, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram spanned by the vectors. A double-angle radial (spherical co-ordinates) operand is coerced to a 3-component vector. The cross-product of two 3-component vectors uses the identity
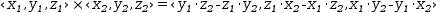
If one of the operands is a matrix, the operator constructs the matrix product (matrix multiplication), coercing the other operands to matrix if necessary.
Equivalence operators produce a Boolean result from tests for equality (=), equivalence (≡), inequality (≠) and approximation (≈). The equivalence operator is functionally the same as the equality operator and is present only for completeness. The approximation operator compares numeric values using a “fuzz factor” to accommodate cumulative round-off error. For operands with different types, the operand with the lower type is coerced to the type of the other operand. For set operands, equality is performed by comparing the result of set difference to the empty set.
Lookup finds the index of the right operand within the left operand. Comparisons are performed using the equality operator. The result of lookup on a tuple is a real; the result of lookup on a matrix is a tuple of two reals. Other left-operand types are not supported. If the right operand cannot be found within the left operand, the result is -1 or the empty tuple.
Numeric
operators provide addition, subtraction, multiplication, division,
quotient modulus, exponentiation and radical operations.
The latter
two are right associative. They are related by
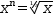
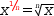
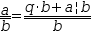
Outer Product. If both operands are vectors, the result is a matrix formed by multiplying each component of the left operand with each component of the right. The rows of the result are determined by the length of the left operand and the columns of the result are determined by the length of the right operand.
If the operands are matrices, the result is a matrix formed by multiplying each component of the left operand by the the right operand. If either operand is matrix, the other is coerced to matrix.
Partition ↓ and ↑ perform drop and take operations on tuples, matrices and strings. The right operand indicates how many items to drop or retain. The right operand can be a singleton tuple or a real that indicates how many elements or characters to drop or retain. It can also be a tuple of two reals; for a left operand that is a tuple or a matrix, the result is a matrix in the shape of the right operand whose values are taken from the left operand; for a left operand that is a string, the result is a substring. See §6.2.3 for more detail on how these operators affect matrices.
Plus or Minus
operators summarize a set of two arithmetic expressions one with plus
and the other with minus. Distributing
a binary ± produces a set:

Protected expressions, no matter how complex, are treated as primaries by all the transformations. The type of the primary is that of the protected expression. The effect of protection is to make the complex expression behave like a simple variable, opaque to recursively applied transformations like simplification. Protected expressions have a distinctive appearance when displayed, using some form of highlighting.
Relational operators produce a Boolean result. Relative comparisons can be used only on operands that are either both real or both string.
Scalar Product
produces the sum of the product of corresponding items in two
length-matched vectors.
Vector product is also known as inner product.
This operator is inferred by the parser for multiply with vector
operands.
That is
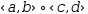
Set operators.
The operators ∪, ∩, ∖ and △ provide union, intersection, set
difference
and symmetric difference operations.
The operators ⊂, ⊆, ⊄,
⊈ provide subset tests that produce Boolean
results.
Tuples are treated
as multisets. When one operand is a tuple and
the other is a set, the
set operand is widened to a multiset.
For multisets,